Convolution Neural Network Tutorial
Introduction
This tutorial will introduce the topic of Convolutional Neural Networks and a run through a brief application. This tutorial will assume a basic knowledge of Neural Networks but will provide a basic review of necessary concepts.
Neural Networks were inspired by the biological neural networks of the brain. Neural Networks are made up of 3 different types of layers: Input Layer, Hidden Layer, Output Layer. Each layer can consist of any number of neurons/nodes
Convolutional Neural Networks are primarily used for analyzing visual imagery - specifically in this tutorial it will be featured in image recognition. CNNs apply a series of filters to the raw pixel data of an image to extract and learn the high-level features. These high-level features can then be used to classify any input image and generate predictions more accurate than humans.
In general, CNNs contain 3 main components:
Convolutional Layers: Apply a specific convolutional filter to the input image and receive another (potentially smaller) output image
Pooling Layers: Used to extract the “important” information from the convolutional layers and reduces the dimensionality of the dataset which can speed up the overall processing time of the program
Fully Connected (Dense) Layers: Performs classification on the features collected by the convolutional and pooling layers
Tutorial Content
In this tutorial, we'll cover the following topics:
Explaining Convolutional Neural Networks
Convolutional Layers
Convolutional layers (conv. layer) are what define CNNs. Every image can be represented as a matrix of pixel values. In the gif, below we have a 5 by 5 image of values and a filter of size 3 by 3. The output, a feature map/convolved feature, is the result of performing the dot product between the image and the filter to every potential group of cells in the image.
Basic example of what happens in a convolutional layer:
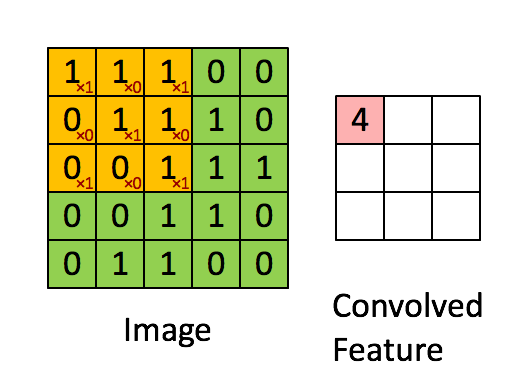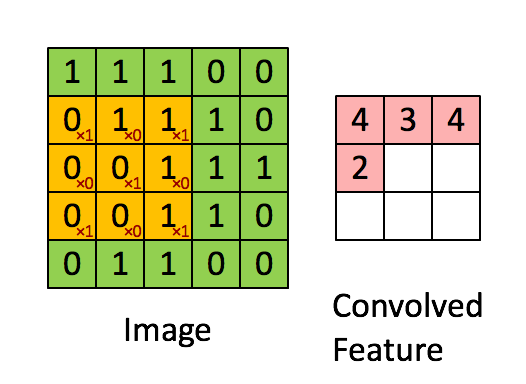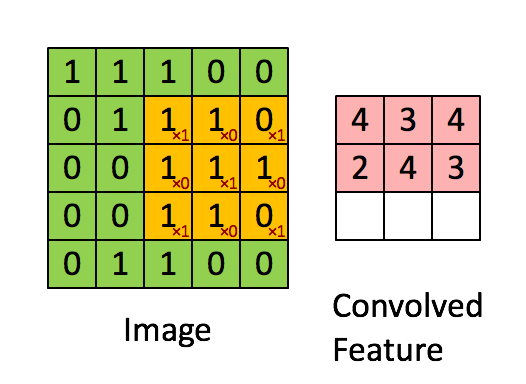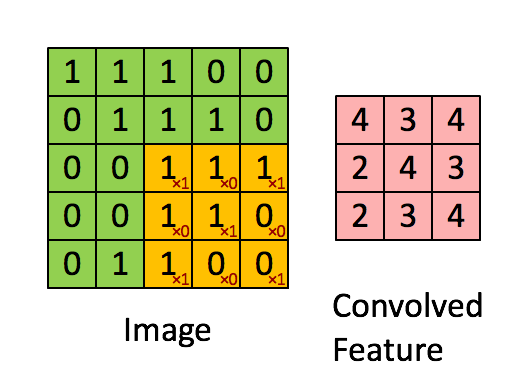
It is important to notice that different values in the filter matrix can produce different feature maps. Prior to CNNs, filters had to be programmatically filled by an expert who understood the field of study the application was to be used in. However, now CNNs can learn the values of these filters during the training step (other paramters must be specified instead like the number of filters, the size of the filter, etc...).
Three of the more important parameters that will be explained in detail are: Depth, Stride, and Padding.
Specifying the depth tells us the number of filters to be used on the input matrix. Imagine for depth > 1 the returned feature maps are stacked on one another so the output of a convolution layer would have shape of feature map by depth parameter.
Specifying the stride tells us number of cells the filter needs to slide over the input matrix. The gif above uses a stride of 1. Having a stride of 2 tells the filter to move over 2 pixels before computing the dot product.
Specifying the padding tells us whether the input matrix should have an additional border of cells with 0s to create a "new" input matrix. When the filter is applied to the enlarged input matrix the new feature map is the same dimension as the original matrix (old 5x5 input → new 7x7 input → 3x3 filter 5x5 feature map).
At the end of every convolution layer we apply a non-linear function to rectify the results of our feature map. In real-world examples, data is hardly ever linear so by introducing non-linearity into the model we can help with overall generalization to testing examples. The common function used for this is the ReLU (Rectified Linear Unit) function whose output is: max(0, input value). This in effect highlights all of the positive pixel values by replacing all the negative pixel values in the feature map with 0s. Other common non-linear functions include: tanh or sigmoid (functions from basic calculus courses).
Pooling Layers
Pooling layers assist with reducing the dimensionality of the feature maps and return the most "important" information. There are many different types of pooling but the main three include: Max, Average, and Sum. In the pooling layer, we apply some of the same techniques as in the convolution layer; for all types of pooling we have an input matrix, a filter, and a stride.
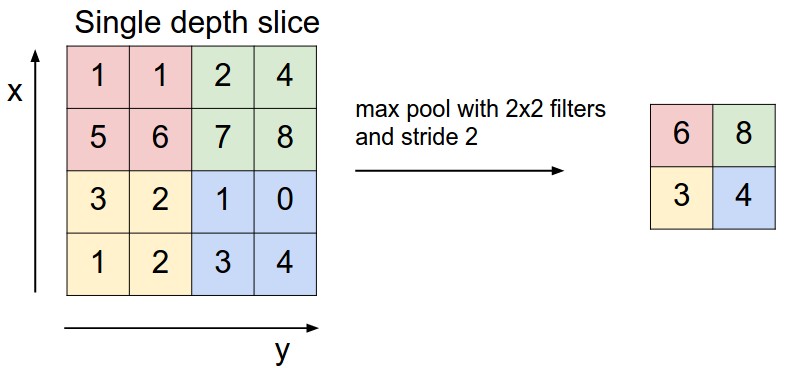
For Max Pooling we have a filter covering somer number of cells in the input matrix. We then take the max of these cells and that becomes one value in our new feature map. In the example below the red in the left matrix is the area covered by the filter and the max of those 4 values is 6 which becomes the top left cell of the feature map. The same type of concept is applied to Sum Pooling (taking the sum of all cells in the filter) and Average Pooling (taking the average of all the cells in the filter).
Fully Connected Layers
Fully connected layers are responsible for using the high-level features of the input image to classify the input image into various classes. These layers assign probabilities to the different potential classes; using a Softmax function which normalizes the integer scores for each class into a value between 0 and 1.
Full Training Process
Initialize all the filters, parameters, weights, etc... with random values
The three types of layers above can be described as the forward propagation step of training in a Neural Network.
The network takes a random training image as input and runs through the forward propagation step and assigns probabilities to each class for said example
Calculate the total error of said training example ∑0.5 ∗ (target prob − output prob)^2
Perform back propagation to calculate the gradients with respect to the weights in the network and update the filters, parameters, and weights to minimize the total error
Repeat 2-4 for every image in the training set
Installing the libraries
First the necessary libraries must be installed for neural networks. There are many different libraries that focus on neural networks (TensorFlow, TFLearn, Blocks, nolearn, etc...) each with their own strengths and weaknesses. This tutorial will focus on one of the more high level libraries called Keras.
Installing Keras on a machine is as simple as running the following command:
$ pip install kerasIt might also be necessary for your machine to have Tensorflow installed which can be done with the following command:
$ pip install tensorflowUpon running those two lines, make sure the following commands work for you in the coding project:
import matplotlib.pyplot as plt
import numpy as np
import keras
from keras import backend as K
from keras.utils import np_utils
if K.backend()=='tensorflow':
K.set_image_dim_ordering('th')
import tensorflow as tf
np.random.seed(42)Loading and understanding the data
The dataset featured in this tutorial is CIFAR-10 which was collected by individuals in University of Toronto. This dataset consists of 60,000 32x32 color images with 10 different label classes and 6000 images per class. The data is primarily split into 50,000 training and 10,000 test images. The 10 different classes are: Airplane, Automobile, Bird, Cat, Deer, Dog, Frog, Horse, Ship and Truck.
The data is included in the keras installation as a part of the datasets. Standard practice for any machine learning is to also create validation data to evaluate the results of your model before you work with you testing data. Thus, the next few lines of code will load the data and create partitions into training (50,000), testing (5,000), and validation (5,000) data (setting the random state to 42 below and above is for reproducibility of this tutorial). The y_train, y_test, and y_valid variables represent the category labels with integers ranging from 0-9 for their respective datasets.
from keras.datasets import cifar10
from sklearn.model_selection import train_test_split
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_test, x_valid, y_test, y_valid = train_test_split(x_test, y_test, test_size = 0.5, random_state = 42)
x_train_shape = 'x_train shape: ' + str(x_train.shape)
x_valid_shape = 'x_valid shape: ' + str(x_valid.shape)
x_test_shape = 'x_test shape: ' + str(x_test.shape)
print(x_train_shape)
print(x_valid_shape)
print(x_test_shape)The resulting output should return:
x_train shape: (50000, 3, 32, 32)
x_valid shape: (5000, 3, 32, 32)
x_test shape: (5000, 3, 32, 32)Now that we've loaded in the data, it is important to understand our inputs to the model. The last line of code above tells us that the data is a numpy array of 50,000 examples as a 3 by 32 by 32 uint8 array of RGB images (0 to 255 for each of the Red, Green, and Blue channels of the image).
It is helpful to transform the x variables into floats and divide by 255 to normalize the inputs for the network. It is also common practice to manipulate our yvariables to an indicator variable representing the class the example belongs to (e.x. print(y_train.shape) should return (50000, 10) and print(y_train[1]) should return [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.], the first data point belongs to the 10th label in the data). The discussed manipulation is done below.
x_train = x_train.astype('float32')[:1000]
x_train /= 255
x_valid = x_valid.astype('float32')[:100]
x_valid /= 255
x_test = x_test.astype('float32')[:100]
x_test /= 255
print('Before manipulation:')
y_train_shape = 'y_train shape: ' + str(y_train.shape)
y_ex = 'y_ex: ' + str(y_train[1])
print(y_train_shape)
print(y_ex)
print('\nAfter manipulation:')
y_train = keras.utils.np_utils.to_categorical(y_train[:1000])
y_valid = keras.utils.np_utils.to_categorical(y_valid[:100])
y_test = keras.utils.np_utils.to_categorical(y_test[:100])
y_train_shape = 'y_train shape: ' + str(y_train.shape)
y_ex = 'y_ex: ' + str(y_train[1])
print(y_train_shape)
print(y_ex)
The resulting output of the code above should be:
y_train shape: (50000, 1)
y_ex: [9]
After manipulation
y_train shape: (1000, 10)
y_ex: [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]Building the network
Upon finishing our data manipulation we can now build our CNN. The code below will just load the necessary layers and details to easily create our network.
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Dropout
from keras.layers import Flatten
from keras.optimizers import SGD
from keras.constraints import maxnorm
from keras.layers.convolutional import Conv2D
from keras.layers.convolutional import MaxPooling2D
First, if we specify the model to be built through the Sequential() method we can add layers intuitively in our code.
In Conv2D() we first specify the depth argument, followed by the size of the filter (x length, y length). We also specify the input shape size, our chosen activation function, and the padding parameter. We have similar patterns to filling out the arguments to MaxPooling2D() and Dense().
There are a few things in the code that were not mentioned above. The Dropout layer is used to randomly select 0.2 of the inputs and set them to 0 during the training time. This is helpful to reduce overfitting in the model.
The Flatten layer is used to flatten the input matrix to a 1 dimensional matrix. In the output of the code below we can see how the shape of the model changes from before and after Flatten().
Lastly, the maxnorm(x) is used for regularization in the network model. If the L2-norm of the weights is greater than x then the matrix of weights is scaled to reduce the L2-norm to value x. Specifically, it appears to improve the network significantly when Dropout() is used.
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (3, 32, 32), activation = 'relu', padding = 'same'))
model.add(Dropout(0.2))
print(model.output_shape)
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same'))
model.add(MaxPooling2D(pool_size=(2, 2)))
print(model.output_shape)
model.add(Conv2D(64, (3, 3), activation = 'relu', padding = 'same'))
model.add(Dropout(0.2))
print(model.output_shape)
model.add(Conv2D(64, (3, 3), activation = 'relu', padding = 'same'))
model.add(MaxPooling2D(pool_size=(2, 2)))
print(model.output_shape)
model.add(Conv2D(128, (3, 3), activation = 'relu', padding = 'same'))
model.add(MaxPooling2D(pool_size = (2, 2)))
print(model.output_shape)
model.add(Flatten())
model.add(Dropout(0.2))
print(model.output_shape)
model.add(Dense(1024, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.2))
print(model.output_shape)
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.2))
print(model.output_shape)
model.add(Dense(y_test.shape[1], activation = 'softmax'))The resulting dimensions of each layer are as follows:
(None, 32, 32, 32)
(None, 32, 16, 16)
(None, 64, 16, 16)
(None, 64, 8, 8)
(None, 128, 4, 4)
(None, 2048)
(None, 1024)
(None, 512)Finally, we can compile the model and review the different components of it in the output of the cell below. Also implemented is a class which is useful in keeping track of the results from the training.
model.compile(loss = keras.losses.categorical_crossentropy,
optimizer = keras.optimizers.SGD(lr = 0.01),
metrics = ['accuracy'])
model.summary()
class AccuracyHistory(keras.callbacks.Callback):
def on_train_begin(self, logs={}):
self.acc = []
def on_epoch_end(self, batch, logs={}):
self.acc.append(logs.get('acc'))
history = AccuracyHistory()
The official summary of each layer in this example Convolutional Neural Network is displayed below:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d_6 (Conv2D) (None, 32, 32, 32) 896
_________________________________________________________________
dropout_6 (Dropout) (None, 32, 32, 32) 0
_________________________________________________________________
conv2d_7 (Conv2D) (None, 32, 32, 32) 9248
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 32, 16, 16) 0
_________________________________________________________________
conv2d_8 (Conv2D) (None, 64, 16, 16) 18496
_________________________________________________________________
dropout_7 (Dropout) (None, 64, 16, 16) 0
_________________________________________________________________
conv2d_9 (Conv2D) (None, 64, 16, 16) 36928
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 64, 8, 8) 0
_________________________________________________________________
conv2d_10 (Conv2D) (None, 128, 8, 8) 73856
_________________________________________________________________
max_pooling2d_6 (MaxPooling2 (None, 128, 4, 4) 0
_________________________________________________________________
flatten_2 (Flatten) (None, 2048) 0
_________________________________________________________________
dropout_8 (Dropout) (None, 2048) 0
_________________________________________________________________
dense_4 (Dense) (None, 1024) 2098176
_________________________________________________________________
dropout_9 (Dropout) (None, 1024) 0
_________________________________________________________________
dense_5 (Dense) (None, 512) 524800
_________________________________________________________________
dropout_10 (Dropout) (None, 512) 0
_________________________________________________________________
dense_6 (Dense) (None, 10) 5130
=================================================================
Total params: 2,767,530
Trainable params: 2,767,530
Non-trainable params: 0
_________________________________________________________________Running and Evaluating the Network
Some final components are necessary to specify before the model begins training. Firstly, we must specify the number of epochs the training has to undergo. An epoch is defined as one forward propogation and one back propogation of all the training examples. Secondly, we must specify the batch size. Batch size is the number of training examples in one foward/backward pass. The larger the batch size, the more memory space the machine will need. For the purpose of this tutorial and quick reproducibility, a very small epoch was defined and a small batch size was defined.
epochs = 2
batch_size = 50
model.fit(x_train, y_train,
batch_size = batch_size,
epochs = epochs,
verbose = 1,
validation_data = (x_valid, y_valid),
callbacks = [history])
score = model.evaluate(x_test, y_test, verbose = 0)
test_str = 'Test data loss: ' + str(score[0])
test_acc = 'Test data accuracy: ' + str(score[1])
print(test_str)
print(test_acc)
Train on 1000 samples, validate on 100 samples
Epoch 1/2
1000/1000 [==============================] - 29s 29ms/step - loss: 2.2682 - acc: 0.1330 - val_loss: 2.2817 - val_acc: 0.1700
Epoch 2/2
1000/1000 [==============================] - 29s 29ms/step - loss: 2.2613 - acc: 0.1520 - val_loss: 2.2750 - val_acc: 0.2300
Test data loss: 2.2795009422302246
Test data accuracy: 0.21
Below is just a plot detailing the change in accuracy as the number of epochs increased
plt.plot(range(1, epochs + 1), history.acc)
all_acc = 'Accuracies: ' + str(history.acc)
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.show()The resulting accuracies for “epoch=1” and “epoch=2” are displayed below:
Accuracies: [0.13299999944865704, 0.151999999769032]
These numbers are particularly great but this is an upward improvement when evaluating such basic parameters. This suggests we could do much better after fine tuning the parameters of interest in the CNN.
Final Thoughts
For me this was an interesting tutorial to experiment more with CNNs. The results of this simple model were okay but still very improvable. To improve the model performance some ideas are: training for more epochs, altering the data inputs before evaluating them with the model, or even appending more layers to the CNN.
Summary and References
This tutorial covered only the basics of Convolutional Neural Networks. The concepts here can be very difficult to explain so some of the detailed parts were simplified. I would highly suggest reading the source documentation for Keras or experimenting with other libraries to find the one that works the best. Below are some links of interest regarding this tutorial.
CIFAR-10 Dataset: https://www.cs.toronto.edu/~kriz/cifar.html
Keras: https://keras.io
Fun Visual of CNNs with MNIST Dataset: http://scs.ryerson.ca/~aharley/vis/conv/flat.html

